Tìm hiểu về giải thuật tham lam
Cấu trúc dữ liệu và giải thuật
Thuật toán tham lam được ứng dụng nhiều rất vào các bài toán thực tế. Hãy cùng mình tìm hiểu nhé...
Thuật toán tham lam là gì, nó có tham lam thật không ???

Nội dung chính







Giới thiệu
Giải thuật tham lam (tiếng Anh: Greedy algorithm) là một thuật toán giải quyết một bài toán theo kiểu metaheuristic để tìm kiếm lựa chọn tối ưu địa phương ở mỗi bước đi với hy vọng tìm được tối ưu toàn cục.
Hiểu một cách đơn giản như sau :
Bây giờ mẹ bạn cho bạn 2 tờ tiền mệnh giá 100.000 đ và 200.000 đ và bạn chỉ được chọn 1. Và đương nhiên mình sẽ chọn tờ 200.000 đ vì nó giá trị hơn mặc dù số lượng và kích thước của 2 tờ đều như nhau.
Một ví dụ khác nhé. Ta có một ba lô có trọng lượng là 37 và 4 loại đồ vật với trọng lượng và giá trị tương ứng, yêu cầu ở đây là bạn sẽ phải chọn tối đa số lượng đồ vật để vừa phù hợp với trọng lượng của ba lô mà giá trị lấy được là lớn nhất.
Từ đó ta có kỹ thuật Tham lam áp dụng cho bài toán này là:
Tính đơn giá cho các loại đồ vật.
Xét các loại đồ vật theo thứ tự đơn giá từ lớn đến nhỏ.
Với mỗi đồ vật được xét sẽ lấy một số lượng tối đa mà trọng lượng còn lại của ba lô cho phép.
Xác định trọng luợng còn lại của ba lô và quay lại bước 3 cho đến khi không còn có thể chọn được đồ vật nào nữa.
Tổng quan về giải thuật
Tham lam là một trong những phương pháp phổ biến nhất để thiết kế giải thuật. Tham lam thường là thuật toán dạng lặp, trong đó tại mỗi bước, ta xây dựng lời giải dần dần, cho đến khi thuật toán lặp kết thúc ta sẽ thu được lời giải cuối cùng của bài toán.
Ý tưởng của tham lam, như cái tên đã gợi ý cho ta, là:
Nguyên lý tham lam
Tại mỗi bước của thuật toán, trong số các lựa chọn khả thi, chọn một lựa chọn có lợi nhất
Rất nhiều thuật toán nổi tiếng được thiết kế dựa trên tư tưởng của tham lam, ví dụ như thuật toán tìm đường đi ngắn nhất của Dijkstra, thuật toán cây khung nhỏ nhất của Kruskal, v.v.
Trong bài này chúng ta sẽ tìm hiểu nguyên lý thiết kế tham lam thông qua một vài ví dụ.
Ví dụ 1
Ta có một ba lô có trọng lượng là 37 và 4 loại đồ vật với trọng lượng và giá trị tương ứng được cho như sau :
| Loại đồ vật | A | B | C | D |
|---|---|---|---|---|
| Trọng lượng | 15 | 10 | 2 | 4 |
| Giá trị | 30 | 25 | 2 | 6 |
Từ bảng đã cho ta tính đơn giá cho các loại đồ vật và sắp xếp các loại đồ vật này theo thứ tự đơn giá giảm dần ta có bảng sau.
| Loại đồ vật | B | A | D | C |
|---|---|---|---|---|
| Trọng lượng | 10 | 15 | 4 | 2 |
| Giá trị | 25 | 30 | 6 | 2 |
| Đơn giá | 2.5 | 2.0 | 1.5 | 1.0 |
Theo đó thì thứ tự ưu tiên để chọn đồ vật là là B, A, D và cuối cùng là C.
Vật B được xét đầu tiên và ta chọn tối đa 3 cái vì mỗi cái vì trọng lượng mỗi cái là 10 và ba lô có trọng lượng 37. Sau khi đã chọn 3 vât loại B, trọng lượng còn lại trong ba lô là 37 – 3*10 = 7. Ta xét đến vật A, vì A có trọng lượng 15 mà trọng lượng còn lại của balô chỉ còn 7 nên không thể chọn vật A. Xét vật D và ta thấy có thể chọn 1 vật D, khi đó trọng lượng còn lại của ba lô là 7-4 = 3. Cuối cùng ta chọn được một vật C.
KẾT LUẬN
Như vậy chúng ta đã chọn 3 cái loại B, một cái loại D và 1 cái loại C. Tổng trọng lương là 310 + 14 + 12 = 36 và tổng giá trị là 325+16+12 = 83.
Thuật toán
Nói chung, giải thuật tham lam có năm thành phần:
Một tập hợp các ứng viên (candidate), để từ đó tạo ra lời giải
Một hàm lựa chọn, để theo đó lựa chọn ứng viên tốt nhất để bổ sung vào lời giải
Một hàm khả thi (feasibility), dùng để quyết định nếu một ứng viên có thể được dùng để xây dựng lời giải
Một hàm mục tiêu, ấn định giá trị của lời giải hoặc một lời giải chưa hoàn chỉnh
Một hàm đánh giá, chỉ ra khi nào ta tìm ra một lời giải hoàn chỉnh.
Có hai thành phần quyết định nhất tới quyết định tham lam:
Tính chất lựa chọn tham lam
Chúng ta có thể lựa chọn giải pháp nào được cho là tốt nhất ở thời điểm hiện tại và sau đó giải bài toán con nảy sinh từ việc thực hiện lựa chọn vừa rồi.
Lựa chọn của thuật toán tham lam có thể phụ thuộc vào các lựa chọn trước đó. Nhưng nó không thể phụ thuộc vào một lựa chọn nào trong tương lai hay phụ thuộc vào lời giải của các bài toán con.
Thuật toán tiến triển theo kiểu thực hiện các chọn lựa theo một vòng lặp, cùng lúc đó thu nhỏ bài toán đã cho về một bài toán con nhỏ hơn. Đấy là khác biệt giữa thuật toán này và giải thuật Quy Hoạnh Động. Giải thuật quy hoạch động duyệt hết và luôn đảm bảo tìm thấy lời giải.
Tại mỗi bước của thuật toán, quy hoạch động đưa ra quyết định dựa trên các quyết định của bước trước, và có thể xét lại đường đi của bước trước hướng tới lời giải.
Giải thuật tham lam quyết định sớm và thay đổi đường đi thuật toán theo quyết định đó, và không bao giờ xét lại các quyết định cũ. Đối với một số bài toán, đây có thể là một thuật toán không chính xác.
Cấu trúc con tối ưu
Một bài toán được gọi là “có cấu trúc tối ưu”, nếu một lời giải tối ưu của bài toán con chứa lời giải tối ưu của bài toán lớn hơn.
Ta có thể thực hiện cài đặt bằng các thủ tục như sau:
- Tính đơn giá của các sản phẩm.
struct DoVat {
char Ten [20];
float TrongLuong, GiaTri, DonGia;
int PhuongAn;//so luong do vat chon
};
- Tính đơn giá của các sản phẩm. Độ phức tạp thuật toán là O(n)
void TinhDonGia(DoVat sp[], int n)
{
for(int i = 1; i <= n; i++)
sp[i].DonGia = sp[i].GiaTri / sp[i].TrongLuong;
}
- Sắp xếp giảm dần theo đơn giá. Độ phức tạp thuật toán O(n2)
void SapXep(DoVat sp[], int n)
{
for(int i = 1; i <= n - 1; i++)
for(int j = i + 1; j <= n; j++)
if (sp[i].DonGia < sp[j].DonGia)
swap(sp[i], sp[j]);
}
- Xác định sản phẩm cần lấy. Độ phức tạp thuật toán là O(n)
void Greedy(DoVat sp[], int n, float W)
{
for (int i = 0; i < n; i++) {
sp[i].PhuongAn = W / sp[i].TrongLuong;
W -= sp[i].PhuongAn * sp[i].TrongLuong;
}
}
Ví dụ 2
Ta sẽ cùng đến với một bài toán thực tế nhé, đây là bài tập đầu tiên khi mình biết đến Thuật toán tam lam.
Đề bài
Xây dựng chức năng đổi tiền với các yêu cầu sau:
Input: Nhập vào số tiền cần đổi
Output: Hiển thị các mệnh giá tiền được đổi ra
Biết rằng: Mệnh giá tiền gồm có: 500, 200, 100, 50, 20, 10, 5, 2, 1
Test case:
| Input | Output |
|---|---|
| 500K | 2 tờ 200K và 1 tờ 100K |
| 234K | 1 to 200K, 1 tờ 100K, 2 tờ 20K và 1 to 2K |
| 9K | 1 to 5K và 2 tờ 2K |
Hãy suy nghĩ cách giải rồi bấm vào xem code của mình dưới đây xem có giống nhau không nhé
SẼ THẬT LÀ TUYỆT
Nếu bạn để lại code của mình phía dưới comment bài viết này ^^
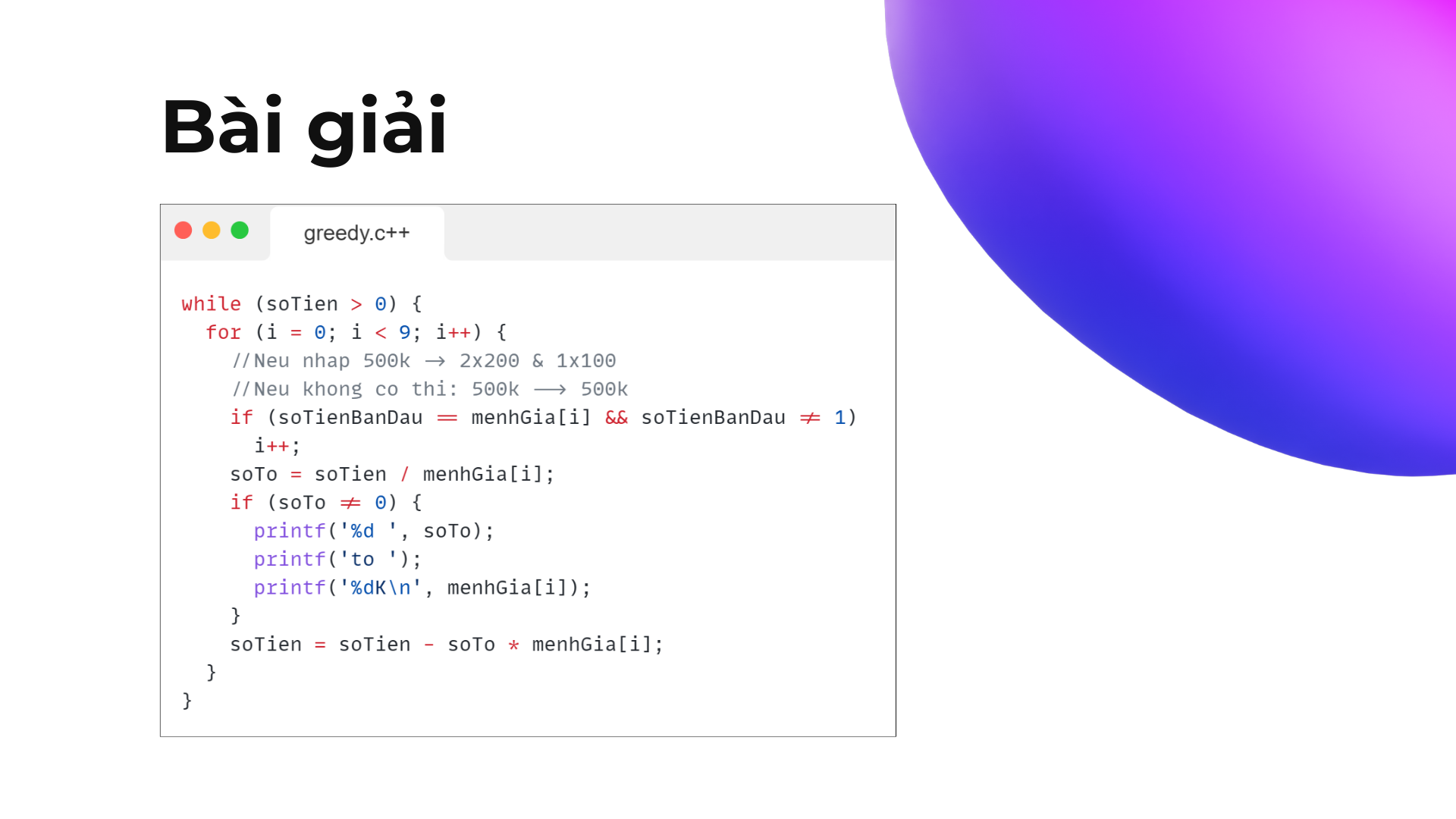
Bài giải
BÀI GIẢI
#include<stdio.h>
int main() {
int i,soTo,soTien,soTienBanDau;
int menhGia[9] = {500,200,100,50,20,10,5,2,1};
do {
printf("Nhap vao menh gia muon doi: "); scanf("%d",&soTien);
soTienBanDau=soTien;
if (soTien>0) {
printf("Voi ");
printf("%dK ",soTienBanDau);
printf("ban co the doi thanh:\n");
}
if (soTienBanDau>=1) {
while (soTien>0) {
for (i=0; i<9; i++) {
//Neu nhap 500k -> 2x200 & 1x100
//Neu khong co thi: 500k --> 500k
if (soTienBanDau == menhGia[i] && soTienBanDau !=1 )
i++;
soTo=soTien/menhGia[i];
if (soTo!=0 ) {
printf("%d ",soTo);
printf("to ");
printf("%dK\n",menhGia[i]);
}
soTien=soTien-soTo*menhGia[i];
}
}
} else printf("Khong co menh gia nay, vui long nhap lai!\n");
}while (soTienBanDau<1);
return 0;
}
Ví dụ 3
Ta sẽ đến với một ví dụ liên quan đến toán học một xíu nhé ^^
Lưu file trên đĩa từ
Bài toán như sau:
Giả sử bạn có file trên đĩa từ trong đó file thứ có dung lượng .
Gọi là một hoán vị của tương ứng với một cách lưu trữ file theo thứ tự .
Để truy cập file , bạn phải duyệt qua tất cả các file .
Do đó chi phí để truy cập file là:
Tìm cách lưu trữ file sao cho việc truy xuất được hiệu quả nhất, biết rằng mỗi file được truy cập đúng 1 lần.
Ví dụ 1:
Giả sử các file đánh số có dung lượng lần lượt là . Nếu ta sắp xếp file theo thứ tự thì chi phí truy nhập là . Nếu ta sắp theo thứ tự thì chi phí truy nhập là .
Ý tưởng của giải thuật tham lam như sau: giả sử ta đang ắp xếp file vào vị trí thứ , để giảm chi phí truy nhập file thứ , ta nên lưu trữ các vị trí bằng các file với tổng dung lượng nhỏ nhất.
Cách lưu nào sẽ thoả mãn tính chất này với mọi ? Đó chính là lưu các file theo thứ tự từ nhỏ đến lớn theo dung lượng.
Trong ví dụ 1, cách lưu có chi phí nhỏ hơn là vì nó là cách lưu theo thứ tự từ nhỏ đến lớn.
Ta có giả mã như sau:
GreedyFileOnTape:
repeat
choose with minimum
write to the tape
until
Tính đúng đắn của thuật toán
Ta sẽ chứng minh cách lưu file theo thứ tự từ nhỏ đến lớn có chi phí nhỏ nhất.
Giả sử tồn tại một cách lưu trữ tối ưu và chỉ số sao cho .
Gọi là chi phí truy nhập của \pi.
Theo định nghĩa, ta có:
Gọi là hoán vị thu được từ bằng cách đổi chỗ và . Ta có:
Do đó, , trái với giả thiết là cách lưu trữ tối ưu.
Phân tích thời gian
Bằng cách thực hiện sắp xếp theo chiều tăng của kích thước file, chúng ta có thể thực thi thuật toán trên trong thời gian O(nlogn).
Tổng kết
Đó là tất cả những gì mình biết về Giải thuật tham lam, mong rằng nó sẽ có ích đến bạn, chúc bạn một ngày làm việc, học tập vui vẻ ^^
Để lại ý kiến của bạn bên dưới nhé!
Liên kết
- Giới thiệu
- Tổng quan về giải thuật
- Ví dụ 1
- Thuật toán
- Tính chất lựa chọn tham lam
- Cấu trúc con tối ưu
- Ví dụ 2
- Đề bài
- Bài giải
- Ví dụ 3
- Tính đúng đắn của thuật toán
- Phân tích thời gian
- Tổng kết
- Liên kết